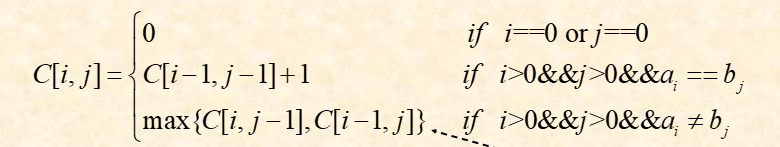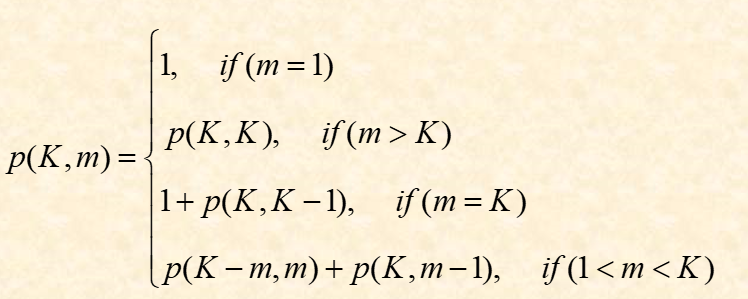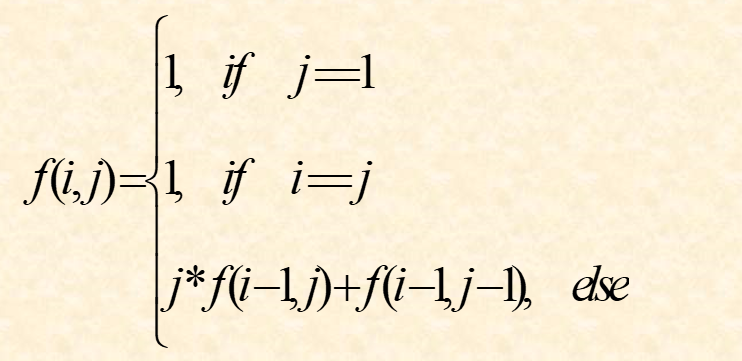1 概述
1.1算法的性质
- 输出
- 输入
- 确定性
- 有穷性
对于一个算法而言上述性质是一定有的,确定性保证了对于一个输入一定仅存在一个输出,有穷性表示了执行次数的有限
程序=算法+数据结构+文档
这里文档可以理解为数据库文件,图片(大型资源),XML文件等程序的配置文件,程序是算法的一个具体实现,但是程序没有规定存在有限性(循环可以为死循环)
1.2 算法的复杂度
对于一个算法的复杂度主要取决于以下三个方面:
- 问题的规模
- 输入
- 算法本身的优劣
对于如今而言,问题的规模在一直的变大,所以我们需要更加优秀的算法,而输入可以理解为一个变量n,表示数据规模的大小,对于一个算法的复杂度,我们可以分为空间复杂度和时间复杂度。由于现在的计算机对于空间的限制大多较少,所以我们主要研究时间复杂度。
1.2.1 时间复杂度
对于一个时间的复杂度,我们主要研究三个情况:
- 最坏情况(最重要,程序的极限)
- 最好情况
- 平均情况
渐进分析:对于T(n)而言,其值为n的单独递增函数,所以为了便于计算,我们只需要找到一个$T^*$(n)保证与T(n)同阶就可以估算T(n)的复杂度
a.四种阶
- O:上界,若$\exist n\geq n_0$,$f(n)\leq C*g(n)$,则称在n足够大时f(n)存在上界,f(n)=O(g(n))
- o:低阶 $\lim_{n\to\infty}\frac{f(n)}{g(n)}=0$,则称f(n)=o(g(n))
- $\Theta$:同阶
- $\Omega$:下界
b.时间复杂度的计算
- 计算迭代次数

- 使用递归公式

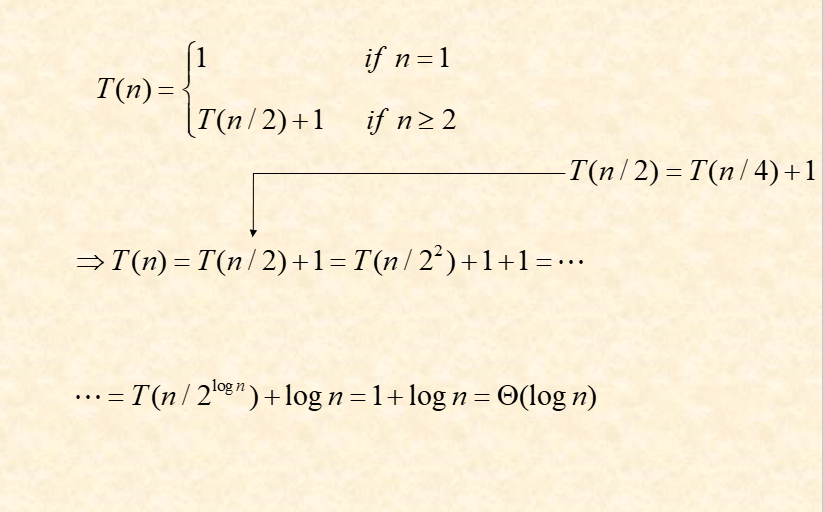
2 数学基础与常用数据结构
2.1 Master Theorem
2.2 递归方程的求解
a.二阶线性同质递归方程求解

使用线代中的特征方程求解
2.3 堆
2.4 不相交集
3 分治算法
3.1 基本思路
将一个问题分为两个不同的部分,之后再合并讨论,所以对于一个分治算法,F(n)与F(n/b)通常满足如下的关系:
$$ F(n)=aF(n/b)+S(n) $$
其中前半部分为每个子问题的时间复杂度,然后相乘,后面的S(n)表示在合并的时候的复杂度
分治算法可以描述为:将一个规模较大的问题分解成若干个规模较小的问题
条件:这些子问题相互独立且与原问题同类
基本模式:
divide_and_conquer(q)
{
if(|P|<=n0)
direct_process(P); //递归的最后
else
{
divide P into P1,P2...Pa;
for(int i=1;i<=a;i++)
{
yi=divide_and_conquer(Pi);
}
merge(y1,y2,...yn);
}
}3.2 矩阵相乘
问题描述:设A,B是两个n*n的矩阵,求C=AB
a.直接相乘
该方法直接利用矩阵的性质直接相乘,这样的话其时间复杂度为$\theta(n^3)$
b.分块矩阵法(直接分治)
思想:将矩阵分为若干个小的矩阵,然后相乘,最后合并
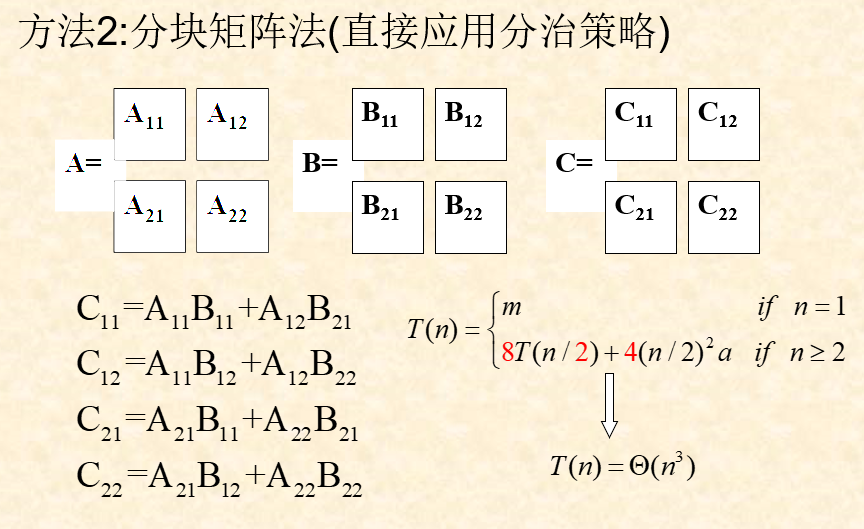
在如上的问题中,可以将矩阵相乘拆分为8个矩阵乘法,同时每一个的规模为之前的1/2,最后需要合并结果,合并的时候需要把分成的4个矩阵再次放在一起
3.3 Strassen’s算法
以上的矩阵乘法的时间复杂度都为$\theta(n^3)$,为了解决该问题采用了优化的矩阵乘法策略

3.4 大数乘法
问题描述:通常使用的乘法中都为小数字的乘法,但是当一个数字非常大的情况,对于二进制乘法而言需要进行很多次的加法操作,所以希望采用分治的策略来对该算法进行优化,同时当计算机中的硬件储存无法完全保存我们乘法中的数字,这样就需要在软件层面对最后的结果进行优化了
算法分析:对于传统的算法,假设为2个nbit的数A,B相乘,那么时间复杂度位$\theta(n^3)$,可以利用计算机中位移运算快于乘法运算的性质直接对问题进行分解

时间复杂度分析:

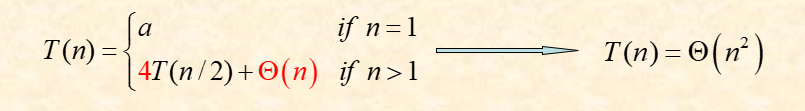
3.5 排列问题
4 动态规划
4.1 引例——费氏数列
递归做法
#include <iostream>
using namespace std;
int fib(int n)
{
if(n==1||n==2)
return 1;
else
return fib(n-1)+fib(n-2);
}该算法的时间复杂度分析可以利用递归式求得,约为$0.477(1.618)^n$,为指数级别,故我们可以改造
该算法的递归过程可以如下:
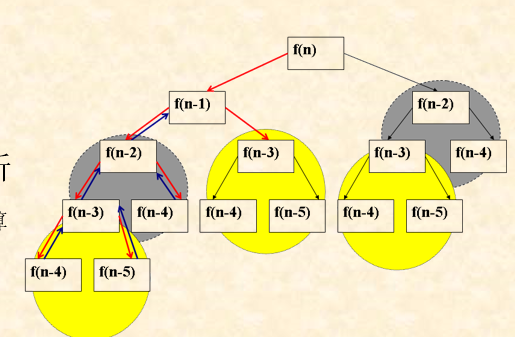
所以存在大量的重复过程,如果我们可以记录重复过程的值,那么就可以将原先的指数级别降低到线性
过程如下:
int f[100]; //假设用于保存前99位的fib数列
int fib(int n)
{
fib[1]=fib[2]=1;
for(int i=3;i<n+1;i++)
{
fib[i]=fib[i-1]+fib[i-2];
}
return fib[n];
}该方法对于fib的过程进行了记录,于是将时间复杂度直接变为了O(n)
4.2 动态规划的基本思想
实质分治与消除冗余,保存子问题的解并且用于之后的计算
使用条件:最优子结构性质
基本步骤:
- 找出最优解的性质,划分子问题
- 递归定义最优解
- 自底向上的方式计算出最优解并且保存
- 得到最优解
4.3 矩阵链相乘
定义:给定n个连乘的矩阵M1,M2,...Mn,问需要最小乘法次数为多少次。
$$ (A)_{p*q}.(B)_{q*r}=p*r*q=p*q*r $$
例如:

不同的矩阵乘法顺序可以出现不同的相乘次数
4.3.1 穷举法
- 找出所有可能相乘方式
- 计算相乘次数
- 找出最小值
对于有n个元素的矩阵,其有$f(n)=\sum_{k=1}^{n-1}{f(k)*f(n-k)}$,最终求得的时间复杂度为$f(n)=\Omega(4^n/n^{1.5})$,时间复杂度过高
4.3.2 动态规划

由以上的结果可以知道,对于一个矩阵的第i个元素到第j个元素的相乘,可以采用该方式进行分开,然后计算合并的时间复杂度。实质为分治算法,由于需要减小时间复杂度,可以考虑把每一个过程记录下来,避免重复计算
/*输入为r[1,2,...,n+1]表示n个矩阵规模的整数*/
int MatrixMul(int r[],int n)
{
/*为了保证与 数学一致,在保存的过程中从1开始保存*/
int C[100][100]; //用于保存初始数据
/*设置对角线,及自身相乘的次数*/
for(int i=1;i<n;i++)
{
C[i][i]=0;
}
/*迭代从链长为2开始一直到n-1*/
for(int i=2;i<=n-1;i++)
{
/*从第一个元素开始迭代*/
for(int j=1;j<=n-i;j++)
{
int m=j+i;//结束元素
C[j][m]=2e31; //设置为极大的数
/*遍历所有的划分*/
for(int k=j+1;k<=m;k++)
C[j][m]=min{C[j][m],C[j][k]+C[k+1][m]+r[j]*r[m+1]*r[k]};
}
}
return C[1][n];
}时间复杂度分析:
其主要的时间复杂度是在于赋值迭代上面,迭代次数为3次,不难发现其时间复杂度为$O(n^3)$.
4.4 0-1背包问题
问题描述:
给定n个物品{u1,u2,...,un}和一个背包,每一个物品对应一个重量wi,以及一个价值vi,背包对应一个承重量C,现在需要选择不超重的物品让最终的背包中的物品价值最高
问题分析:
对于每一个物品,存在两种情况,要么放入背包,要么没有放入背包,那么该问题可以得到如下的公式描述
$$ max\sum_{i=1}^nv_ix_i\\ s.t\;\;\sum_{i=1}^nw_ix_i\leq C,\;x_i\in\{0,1\} $$
对于该问题我们可以进行一个转化,具体如下:
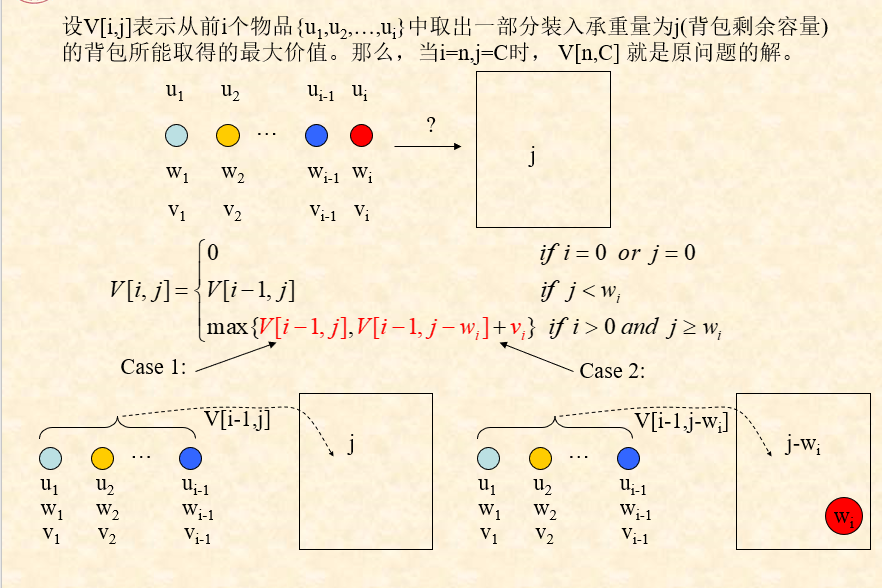
可以理解为,对于一个问题,其解要么和只有i-1个元素的解一样,要么为选择第i个之后的元素相同,上述表达式中的V[i-1,j-wi]+vi可以理解为因为需要选择第i个物品,需要在之前的选择中删除一个物品,所以我们删除价值最低的物品。
C++描述如下:
/*
该题目的输入为物品数目,价值,重量,以及背包的承重
输出为最大的价值,如果需要过程仅仅需要输出过程即可。
*/
int Pack(int n,int w[],int v[],int C)
{
int V[100][100];
/*表达式中的第一种情况*/
for(int i=0;i<=n;i++)
V[i][0]=0;
for(int j=0;j<=C;j++)
V[0][j]=0;
/*递归求得表达式的值*/
for(int i=1;i<=n;i++)
{
for(int j=1;j<=C;j++)
{
V[i][j]=max{V[i][j-1],V[i-1][j-w[i]]+v[i]}; //这里使用伪代码表示选择其中最大的
}
}
return V[n][C];
}时间复杂度分析:
$T(n)=\theta(nC)$
4.5 最长公共子序列问题
问题描述:
给定两个定义在字符集上的字符串A,B,长度分别为n,m,现在要求他们的最长公共子序列的长度值以及对应的子序列
1. Brute-Force
- 找出A字符串的可能序列($2^n$)
- 对于A中的每一个序列判断是否为B的子序列($\Theta(m)$)
- 求max($\Theta(m2^n)$)
2.动态规划
定义C[i][j]为A的前i位与B的前j位的匹配结果,那么可以得到如下的表达式:
当i与j都为0的时候,匹配位数为0位,当最后的1位匹配的时候,结果为分别减少1之后的匹配(可以理解为查看$a_{i-1}?=b_{i-1}$)
int longest(char A[],char B[])
{
int n=strlen(A);
int m=strlen(B);
int C[100][100];
for(int i=0;i<=n;i++)
C[i][0]=0;
for(int i=0;i<=m;i++)
C[0][i]=0;
for(int i=1;i<=n;i++)
{
for(int j=1;j<=m;j++)
{
if(A[i]==B[j])
C[i][j]=C[i-1][j-1]+1;
else
{
C[i][j]=max{C[i-1][j],C[i][j-1]};
}
}
}
return C[n,m];
}时间复杂度分析:
$\theta(nm)$
4.6 整数划分问题
问题描述:将正整数K表示为p个整数的和:
$K=k_1+k_2+...+k_p$,这种表示叫做K的一个划分,现在需要一种算法求出一个正整数的划分数
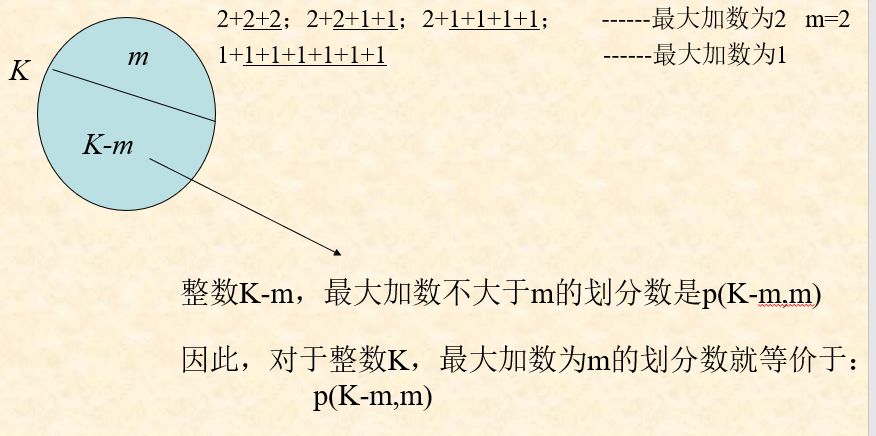
算法分析:定义一个函数$P(K,m)$表示一个最大加数不大于m的划分数目,那么对于K的总共划分数为$P(K)=P(K,K)$,对于该表达式可以列出以下的状态表达式
以此可以看出,但m为1的时候,那么划分只有K个1相加,当m>K的时候,结果同P(K,K)一致,当m=K时,划分数目为K-1以及K本身,其他情况可以将结果划为两个部分,一个部分为m-1的划分,一个为m的划分,具体可以如图:
/*递归写法,非动态规划*/
int P(int K,int m)
{
if(m==1)
return 1;
else if(m>K)
return P(K,K);
else if(m==K)
return 1+P(K,m-1);
else
return P(K-m,m)+P(K,m-1);
}/*动态规划*/
int P(int K,int m)
{
int P[100][100];
for(int i=0;i<=K;i++)
P[i][1]=1;
for(int i=2;i<=m;i++)
{
for(int j=2;j<=K;j++)
{
if(i>j)
P[j][i]=p[j][j];
else(i==j)
P[j][i]=1+p[j][i-1];
else
p[j][i]=p[j-i][i]+p[j][i-1];
}
}
return p[K][m];
}4.7 集合划分问题
问题描述:
给定一个集合X,求X的划分数目
算法分析:
f(i,j)表示集合前i个元素划分为j个子集的划分数,那么对于n个元素的划分数$F(n)=\sum_{i=1}^nf(n,i)$,所以我们需要分析任意的f(i,j)的求法。
对于最后一个可以理解为对于第i个元素,要么单独划分,要么与前面i-1个元素划分到一起,假如单独划分,那么前面i-1个元素划分为j-1个集合,那么为f(i-1,j-1),假如和前面的划分到一起,那么前面的i-1个元素可以划分为j个集合,第i个元素随机加入到前面的集合中,总共有j种加入方式,那么有j*f(i-1,j)种可能
/*动态规划写法*/
int Partion(int n)
{
int p[100][100];
for(int i=0;i<=n;i++)
{
p[i][1]=1;
}
for(int i=0;i<=n;i++)
{
for(int j=0;j<=i;j++)
{
if(i==j)
p[i][j]=1;
else
p[i][j]=j*p[i-1][j]+p[i-1][j-1];
}
}
return sum(p[n]);
}4.8 动态编辑
问题描述:设A与B为两个字符串,要用最少的操作让A变化为B,操作包含如下:
- 删除一个字符
- 插入一个字符
- 将一个字符改为另一个字符
算法分析:定义一个函数d(A,B)表示将A转化为B所需要的最少步骤,那么我们采用动态规划可以得到如下的式子
int replace(int m,int n,char A[],char B[])
{
int d[100][100];
for(int i=0;i<=m;i++)
d[i][0]=i; //删除i位
for(int j=0;j<=n;j++)
d[0][j]=j; //添加j位
for(int i=1;i<=n;i++)
{
for(int j=1;j<=m;j++)
{
if(A[i]==B[j])
d[i][j]=d[i-1][j-1];
else
{
d[i][j]=min{d[i-1][j]+1,d[i][j-1]+1,d[i-1][j-1]+1};
}
}
}
return d[m][n];
}