1. Some basic conception
2. Stream Cipher
2.1 Cipher definition
(keys,messages,cipher-texts)
a pair of "efficient" (E,D)
E: K x M ->C D: K x C->M
D(k,E(K,m))=m
efficient: runs in limited time and can be solved
E is often randomized
D is always deterministic
The one Time Pad: key is to long
2.2 Information Theoretic Security
CT should reveal no "info" about PT
Given CT can't tell if msg is m0 or m1 for all m0 and m1(No CT only attack)
How to prove a Cipher is Security?
$$ P[E(k,m_0)=C] = P[E(k,m_1)=c](|m_0|=|m_1|,\forall c\in C) $$
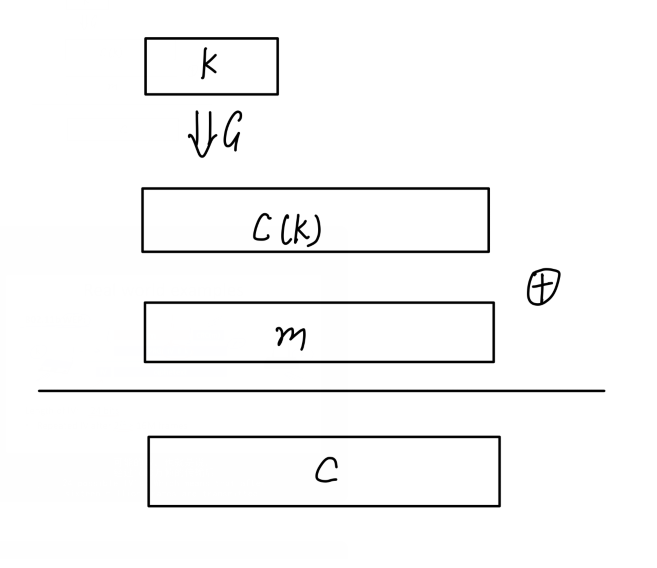
2.3 Stream Cipher
2.3.1 idea
idea: replace "random" key by "pseudo random" key
PRG is a function and have such way
$$ G:\lbrace0,1\rbrace^s ->\lbrace0,1\rbrace^n,n>>s $$
2.3.2 Security
Stream Cipher can't have perfect secrecy
PRG must be unpredictable(predict following bit just by having bit)
Assume a process of sending Email, we know the message begin with From... and then if we can XOR the prefix with the cipher-text. Then we can get the prefix of G(k),if PRG is predictable , then we can get the following message just depend on the prefix
the definition of unpredictable
$$ \exists A: P[A(G(k)|_{1,2,...i}=G(k)|_{i+1,i+2,...,n}]=1/2+\epsilon(\epsilon>0) $$
$$ Practical:non-neg:\epsilon > 1/2^{30}(likely\;to\;happen\;over\;1GB\;of\;data) $$
$$ negligible:\epsilon<1/2^{80}(won't\;happen\;over\;life\;of\;key) $$
2.4 Attack on OTP and Stream Ciphers
2.4.1 Two Time pad is in secure
$$ m_1 \oplus PRG(K)->C_1\; and\; m_2 \oplus PRG(K)->C_2 $$
For attackers:
$$ C_1\oplus C_2->m_1\oplus m_2 $$
For ASCII coding, just have 95 char can be seen,so we can reduce the msg with such way
Example:
- Project Venona(1941-1946)
- MS-PPTP (windows NT) key were the same in the client and service
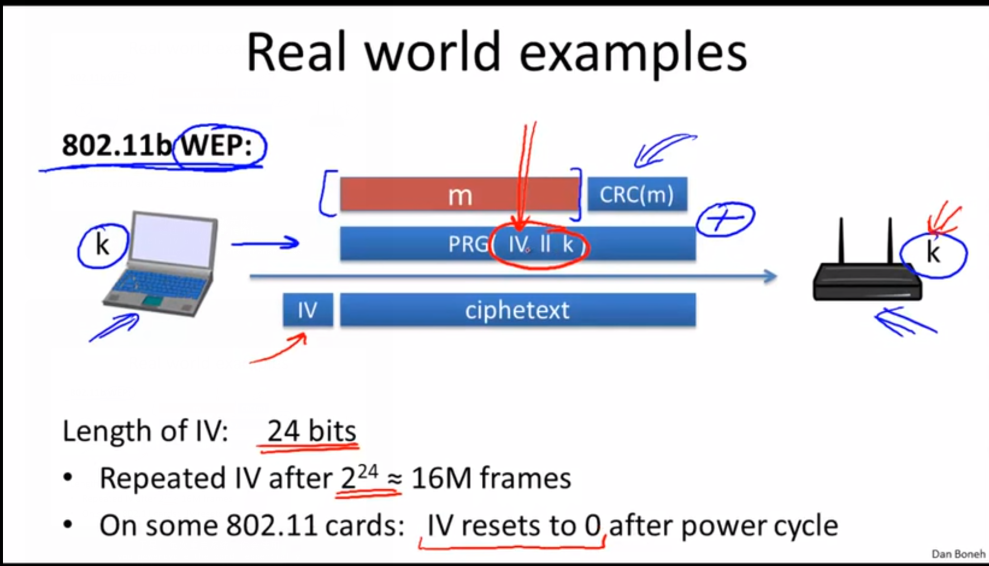
- 802.11b WEP